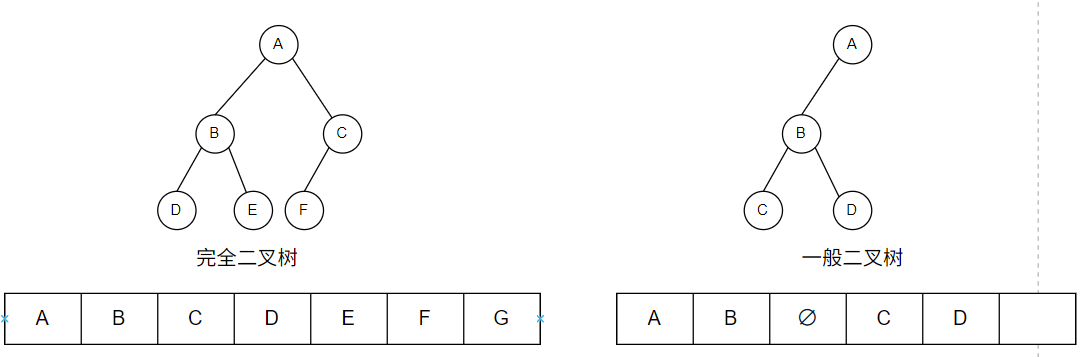
树

普通树

树是n(n>=0)个结点的有限集合

​ 当n=0时, 集合为空,称为空树

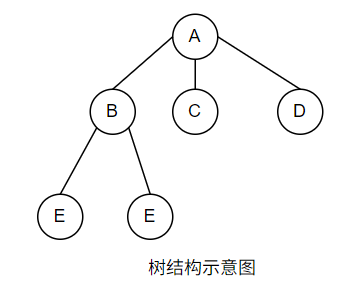
image-20250601170400880

二叉树

二叉树和普通树的区别在于, 二叉树中结点的子树分为左子树和右子树,如下

image-20250601170839340

满二叉树与完全二叉树

如果一个树的层数为K,结点总数为2^k-1个,则它就是满二叉树

在一个深度为h的二叉树中,除第h层(最后一层)外,其他各层都是满的, 并且第h层所有结点都必须从左到右依次放置,不能留空,则它就是完全二叉树

image-20250601172030872

二叉树的性质

  1. 在二叉树的第i层上最多有**2(i-1) **个结点(i>=1)
  2. 深度为k的二叉树最多有2k-1个结点
  3. 任何一个二叉树,如果叶子结点数为n0, 度为2的结点数为n2, 则 n0 = n2+1
  4. 具有n个结点的完全二叉树的深度为[logn2n] + 1

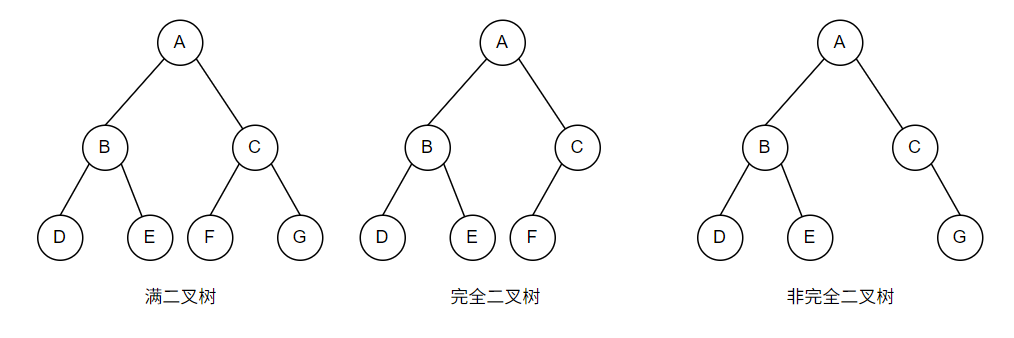
二叉树的存储

  1. 二叉树的顺序存储.在采用顺序存储时,完全二叉树与一般二叉树相比节省了空间,这是因为一般二叉树需要添加一些"虚节点"而造成了空间的浪费

image-20250601181007504